Last April, within the framework of our General Assembly in Foz do Iguaçu, I had the pleasure of moderating a panel on alternative dispute resolution. A little to put a good vibe to the topic, another to give the opportunity to those who arrived just at the session to get the translation teams, and a lot to illustrate the topic, I invited one of the colleagues to participate in an instance of the famous Rock, paper, scissors. In a forced manner, and at the convenience of one of the players (me, obviously), I took the game to the conflict, with the intention of resolving it later using an alternative mechanism, in our case, a decentralized arbitration.

The game that day motivated me to try an approach to the problem of compliance, conflicts and their resolution, under the theory of games. Surely someone already did it, even with better math than mine[1][2], but I think that, from the perspective of the tax administration and the managed taxpayer, it is well worth the exercise.

To facilitate this analysis, it is necessary to assume a considerable set of very gross simplifications, which include disregarding the effect that tax rates could have on compliance – do you remember Laffer[3]? -, the benefits that the taxpayer obtains from the State, social responsibility, transparency, reputational damages and even the fact that someone pays and wants to pay their taxes simply because they consider that it is the minimum cost they have to pay to live in a civilized society[4].

In this case, the rationality of the agent is exclusively determined by the economic benefit or harm that may result from non-compliance. And from that point of view, we visualize it from the point of view of game theory. In the simplest case, assuming an inoperative tax administration, which does not control at all, the “reward” of the game is shown in the table below.

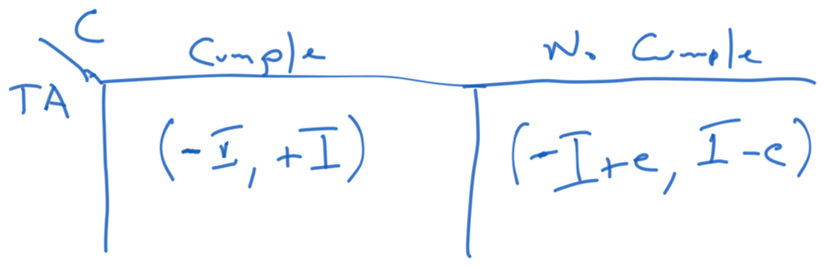
Where I it is the amount that the taxpayer would have to pay, and the one that the tax administration receives, and e, the amount that the taxpayer “earns” by evading, and the one that the tax administration stops receiving. This instance shows us a zero-sum game, under the rationality of obtaining the highest reward the taxpayer will evade, because whenever I > e > 0, you will be paying less tax and increasing your profit. As an example, if the taxpayer should pay 1000 and does so, he has a result of -1000, the administration of +1000; while if he evades, for example, 800, the taxpayer will have a result of -200, which is the same that the administration would receive.

But, of course, the tax administration also plays a role. And can audit and the final result depends on whether the taxpayer complies or not and whether the administration proceeds to auditing, or not:

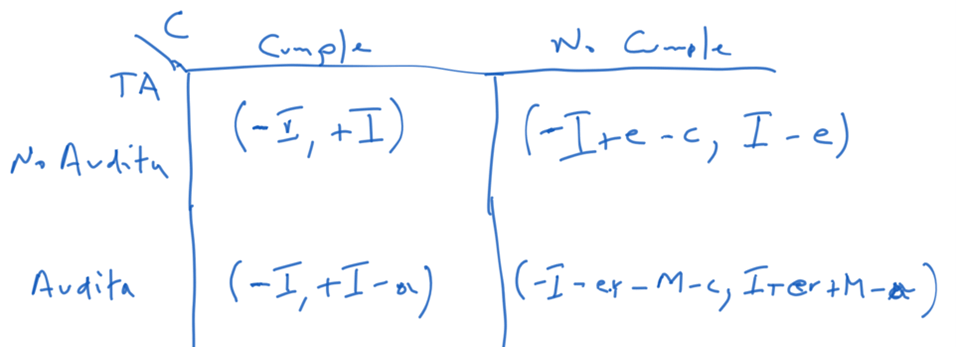
Thus, if the taxpayer complies and the administration does not audit, things remain as in the previous scenario, however, if the taxpayer complies and the administration audits, the effect for the taxpayer is innocuous, but the administration has to cover the cost a of the audit. Which makes us think, once again, under the exclusive rationality of the reward in the game, that the administration should never audit a taxpayer when the audit costs more than the tax that the taxpayer has to pay.

When the taxpayers know that the tax administration can audit, they must, in order to evade, simulate, hide operations, falsify documents, which would have a cost c. This also makes us think that the taxpayer should never evade when the cost of breaching is greater than or equal to the amount to be evaded. Assuming that the cost of evading is 5% of the evaded tax and the cost of the audit is 50, in our example, in which the taxpayer evades 800 and the administration does not audit, the result for the taxpayer would be -1000 +800 – 800×5% = -240; and for the administration 200. The game is no more zero sum.

Where things change significantly is when the taxpayer evades and the tax administration audits, in this case, the taxpayer will end up paying the tax that would correspond to him, increased with the surcharge interest, he will also pay the amount of the fine that corresponds to him and he will have to assume the cost of the breach. The administration will receive the tax with the surcharge, the amount but must deduct the cost of the audit itself. For our example, we also assume here that the surcharge amount is 100% and the fine 100. The result for the taxpayer would be -1000 – 800×100% – 100 – 800×5% = -1000 – 800 – 100 – 40 = – 1940, and for the administration 1000 + 800 + 100 – 50 = 1850.

Or illustrating in the following table:

As surcharges and fines significantly affect the result, high fines and surcharges encourage compliance by the taxpayer because, if they do not comply and are audited, their result will be extremely negative, while if they do not comply and are not audited, their benefit is very great. This means that for the taxpayer, when the tax administration exists, his strategy depends on what the tax administration does. For the administration, on the other hand, as long as the amount of the tax is greater than the cost of the audit, it is convenient to audit, no matter what the taxpayer does.

However, we know, the tax administration cannot audit all taxpayers, there are not enough resources for that. Therefore, for our analysis, the tax administration can audit the taxpayer with a probability p, and consequently there is a probability (1-p) not to be audited. We also know that not necessarily all audits are successful and conclusive, so we could identify as q, to the probability that the tax administration will find the non-compliance in the audit and (1-q) that it will not find non-compliance even via auditing.

With those considerations, the expected reward value for the taxpayer in the event of complying would be:

 (-I×(1-p))+(-I)×p)  or just -I

And the expected value in case of breach would be:

(-I+e-c)×(1-p)+((-I+e-c)×(1-q)+(-I-er-M-C)×q)×p

The following table presents the expected value for the taxpayer who decides to evade, according to the probability values p and q, for selected values of those probabilities.

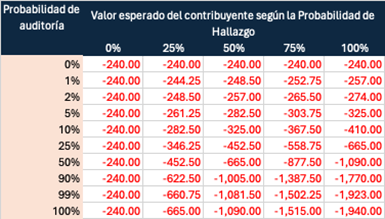
In the event that the probability p of audit is 0, i.e., no one is audited, or that the probability q, of finding and acting on the non-compliance is 0. The expected value of ‑240 matches that of Table 1. Also, the value of -1940 matches that of Table 1, if p and q they are 1, that is, 100% of the taxpayers are audited and 100% of the findings are reached during the audit.

In the other cases we see the expected value for the taxpayer with different probabilities. 1% or 2% probability of audit are included, values more or less corresponding to what would be obtained by the frequency distribution alone between the audited taxpayers and the total of taxpayers in most tax administrations. The effectiveness of audits between 0 and 100%, with 0%, the administration finds nothing, up to 100%, the administration finds everything, and intermediate values. If the administration does not do risk management so that the probability of being audited is much higher for those who evade than for those who behave well, it will be a particularly good business to evade.

For the taxpayer to decide not to evade, the probability of audit has to be, in our example, at least 50%, then the taxpayer begins to find that to pay the tax that correctly corresponds to him is the better business.

To influence the behavior of the taxpayer, considering that fees, surcharges and fines pass by law; it is up to the administration to improve its risk management, for which it has options, ranging from the analysis of the variables and financial ratios of the taxpayer compared to other taxpayers; the incorporation and use of third-party information; the management of complaints and, certainly, the continuous control of transactions, including electronic invoicing and other documents such as withholding certificates or donations. It is also up to the administration to improve the quality of its control capacity and its audits, including the pre-filling of declarations. And generate the conditions so that the cost of non-compliance is extremely expensive, for the taxpayer and for those who help him.

Of course, you already knew all that without reading this post. This is just a confirmation of those concepts from game theory.

And if we are going to start splitting hairs, it would be necessary to include the probability that the administration finds a non-compliance that does not exist, i.e. results in a determination that goes beyond what the taxpayer owes (something that we know the administrators deny, while the taxpayers allege in all cases). Arguments that, by the way, to a large extent, open space for conflict.

This is because, after the breach, the next game comes, to settle the administrative act or discuss it administratively, or in judicial proceedings, or to seek an alternative solution to the conflict. These strategies on the part of the taxpayer and the administration can also be analyzed under the same game theory approach, considering the costs, deadlines and the quality of the decisions of the third parties in charge. Their analysis will determine the strategies, mixed or dominant, of these actors in case of conflict. But that will be for another day’s discussion.

Greetings and good luck

[1] BECKER, G., 1968. “Crime and Punishment: An Economic Approach”, Journal of Political Economy, Vol. 76, No. 2, pp. 169-217.

[2] ALLINGHAM, M. and A. SANDMO, 1972. “Income Tax Evasion: A Theoretical Analysis”, Journal of Public Economics, Vol. 1, Nos. 3-4, pp. 323-338.

[3] https://es.wikipedia.org/wiki/Curva_de_Laffer

[4] Oliver Wendel Holmes Jr. 1904.

1,798 total views, 54 views today